
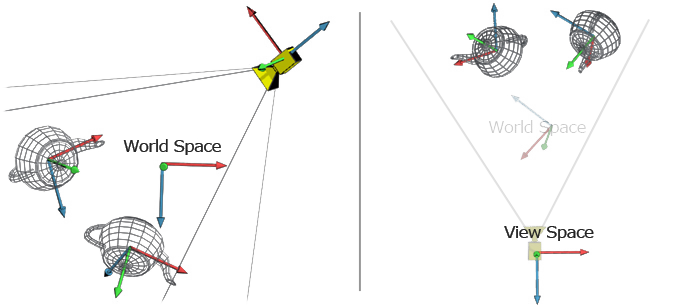
It's important to understand that a vector only makes sense within a coordinate system if we don't specify the space we can't represent any point. All the vertices are relative to the origin of the Model Space, so if we have a point at coordinates (1,1,1) in Model Space, we know exactly where it is (Figure 2).Įvery model in the game lives in its own Model Space and if you want them to be in any spatial relation (like if you want to put a teapot over a table) you need to transform them into a common space (which is what is often called World Space).įigure 1:Standard Right Handed 3D Coordinate Systemįigure 2:Vertex of the teapot in position (1,1,1)

When an artist authors a 3D model he creates all the vertices and faces relatively to the 3D coordinate system of the tool he is working in, which is the Model Space. Vector spaces is quite a broad topic, and it's not the goal of this article to explain them in detail, all we need to know for our purposes is that our models live in one specific vector space, which goes under the name of Model Space and it's represented with the canonical 3D coordinates system (Figure 1). These base vectors can be scaled and added toghether to obtain all the other vectors in the space. Vector Spaces: Model Space and World SpaceĪ vector space is a mathematical structure that is defined by a given number of linearly independent vectors, also called base vectors (for example in Figure 1 there are three base vectors) the number of linearly independent vectors defines the size of the vector space, therefore a 3D space has three base vectors, while a 2D space would have two. From there we will show the typical sequence of transformations that you will need to apply, which is from Model to World Space, then to Camera and then Projection. We will first talk about the relationship between transformations and vector spaces. Then we will show how a transformation can be represented in matrix form.

I will assume general knowledge of vectors math and matrices math. We will try to enter into the details of how the matrices are constructed and why, so this article is not meant for absolute beginners. In this article we will try to understand in details one of the core mechanics of any 3D engine, the chain of matrix transformations that allows to represent a 3D object on a 2D monitor. Thanks to this wikipedia image which makes clear everything about matrix transformation.Article - World, View and Projection Transformation Matrices It combine multiple transform properties into single matrix function. Linear transformations also can be represented by Matrix function. CSS Transform property allows to scale, rotate, skew and move HTML elements.ġ) Scale - resize elements(small or bigger)ģ) Skew - transformation along the X or Y axisĤ) Translate - move element in XY direction


 0 kommentar(er)
0 kommentar(er)
